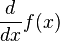Kalkulus (
Bahasa Latin:
calculus, artinya "batu kecil", untuk menghitung) adalah cabang ilmu
matematika yang mencakup
limit,
turunan,
integral, dan
deret takterhingga. Kalkulus adalah ilmu mengenai perubahan, sebagaimana
geometri adalah ilmu mengenai bentuk dan
aljabar adalah ilmu mengenai pengerjaan untuk memecahkan persamaan serta aplikasinya. Kalkulus memiliki aplikasi yang luas dalam bidang-bidang
sains,
ekonomi, dan
teknik; serta dapat memecahkan berbagai masalah yang tidak dapat dipecahkan dengan
aljabar elementer.
Kalkulus memiliki dua cabang utama,
kalkulus diferensial dan
kalkulus integral yang saling berhubungan melalui
teorema dasar kalkulus. Pelajaran kalkulus adalah pintu gerbang menuju pelajaran matematika lainnya yang lebih tinggi, yang khusus mempelajari
fungsi dan
limit, yang secara umum dinamakan
analisis matematika.
Sejarah

Sir Isaac Newton adalah salah seorang penemu dan kontributor kalkulus yang terkenal.
Perkembangan
Sejarah perkembangan kalkulus bisa ditilik pada beberapa periode zaman, yaitu
zaman kuno,
zaman pertengahan, dan
zaman modern. Pada periode zaman kuno, beberapa pemikiran tentang kalkulus integral telah muncul, tetapi tidak dikembangkan dengan baik dan sistematis. Perhitungan
volume dan luas yang merupakan fungsi utama dari kalkulus integral bisa ditelusuri kembali pada
Papirus Moskwa Mesir (c. 1800 SM). Pada papirus tersebut, orang Mesir telah mampu menghitung volume
piramida terpancung.
[1] Archimedes mengembangkan pemikiran ini lebih jauh dan menciptakan
heuristik yang menyerupai
kalkulus integral.
[2]
Pada zaman pertengahan, matematikawan
India,
Aryabhata, menggunakan konsep kecil tak terhingga pada tahun
499 dan mengekspresikan masalah astronomi dalam bentuk
persamaan diferensial dasar.
[3] Persamaan ini kemudian mengantar
Bhāskara II pada abad ke-12 untuk mengembangkan bentuk awal
turunan yang mewakili perubahan yang sangat kecil takterhingga dan menjelaskan bentuk awal dari "
Teorema Rolle".
[4] Sekitar tahun
1000, matematikawan
Irak Ibn al-Haytham (Alhazen) menjadi orang pertama yang menurunkan rumus perhitungan hasil jumlah pangkat empat, dan dengan menggunakan
induksi matematika, dia mengembangkan suatu metode untuk menurunkan rumus umum dari hasil pangkat integral yang sangat penting terhadap perkembangan kalkulus integral.
[5] Pada abad ke-12, seorang
Persia Sharaf al-Din al-Tusi menemukan
turunan dari
fungsi kubik, sebuah hasil yang penting dalam kalkulus diferensial.
[6] Pada abad ke-14,
Madhava, bersama dengan matematikawan-astronom dari
mazhab astronomi dan matematika Kerala, menjelaskan kasus khusus dari
deret Taylor[7], yang dituliskan dalam teks
Yuktibhasa.
[8][9][10]
Pada zaman modern, penemuan independen terjadi pada awal abad ke-17 di Jepang oleh matematikawan seperti
Seki Kowa. Di Eropa, beberapa matematikawan seperti
John Wallis dan
Isaac Barrow memberikan terobosan dalam kalkulus.
James Gregory membuktikan sebuah kasus khusus dari
teorema dasar kalkulus pada tahun 1668.

Gottfried Wilhelm Leibniz pada awalnya dituduh menjiplak dari hasil kerja Sir Isaac Newton yang tidak dipublikasikan, namun sekarang dianggap sebagai kontributor kalkulus yang hasil kerjanya dilakukan secara terpisah.
Leibniz dan
Newton mendorong pemikiran-pemikiran ini bersama sebagai sebuah kesatuan dan kedua orang ilmuwan tersebut dianggap sebagai penemu kalkulus secara terpisah dalam waktu yang hampir bersamaan. Newton mengaplikasikan kalkulus secara umum ke bidang
fisika sementara Leibniz mengembangkan notasi-notasi kalkulus yang banyak digunakan sekarang.
Ketika Newton dan Leibniz mempublikasikan hasil mereka untuk pertama kali, timbul kontroversi di antara matematikawan tentang mana yang lebih pantas untuk menerima penghargaan terhadap kerja mereka. Newton menurunkan hasil kerjanya terlebih dahulu, tetapi Leibniz yang pertama kali mempublikasikannya. Newton menuduh Leibniz mencuri pemikirannya dari catatan-catatan yang tidak dipublikasikan, yang sering dipinjamkan Newton kepada beberapa anggota dari
Royal Society.
Pemeriksaan secara terperinci menunjukkan bahwa keduanya bekerja secara terpisah, dengan Leibniz memulai dari integral dan Newton dari turunan. Sekarang, baik Newton dan Leibniz diberikan penghargaan dalam mengembangkan kalkulus secara terpisah. Adalah Leibniz yang memberikan nama kepada ilmu cabang matematika ini sebagai kalkulus, sedangkan Newton menamakannya "The science of fluxions".
Sejak itu, banyak matematikawan yang memberikan kontribusi terhadap pengembangan lebih lanjut dari kalkulus.
Kalkulus menjadi topik yang sangat umum di SMA dan universitas zaman modern. Matematikawan seluruh dunia terus memberikan kontribusi terhadap perkembangan kalkulus.
[11]
Pengaruh penting
Walau beberapa konsep kalkulus telah dikembangkan terlebih dahulu di Mesir, Yunani, Tiongkok, India, Iraq, Persia, dan Jepang, penggunaaan kalkulus modern dimulai di
Eropa pada abad ke-17 sewaktu
Isaac Newton dan
Gottfried Wilhelm Leibniz mengembangkan prinsip dasar kalkulus. Hasil kerja mereka kemudian memberikan pengaruh yang kuat terhadap perkembangan
fisika.
Aplikasi kalkulus diferensial meliputi perhitungan
kecepatan dan
percepatan,
kemiringan suatu kurva, dan optimalisasi. Aplikasi dari kalkulus integral meliputi perhitungan
luas,
volume,
panjang busur,
pusat massa,
kerja, dan
tekanan. Aplikasi lebih jauh meliputi
deret pangkat dan
deret Fourier.
Kalkulus juga digunakan untuk mendapatkan pemahaman yang lebih rinci mengenai ruang, waktu, dan gerak. Selama berabad-abad, para matematikawan dan filsuf berusaha memecahkan paradoks yang meliputi pembagian bilangan dengan nol ataupun jumlah dari deret takterhingga. Seorang filsuf Yunani kuno memberikan beberapa contoh terkenal seperti
paradoks Zeno. Kalkulus memberikan solusi, terutama di bidang limit dan deret takterhingga, yang kemudian berhasil memecahkan paradoks tersebut.
Prinsip-prinsip dasar
Limit dan kecil tak terhingga

Artikel utama untuk bagian ini adalah:
Limit 
Definisi limit: kita katakan bahwa limit f(x) ketika x mendekati titik p adalah L apabila untuk setiap bilangan ε > 0 apapun, terdapat bilangan δ > 0, sedemikian rupanya:

Kalkulus pada umumnya dikembangkan dengan memanipulasi sejumlah kuantitas yang sangat kecil. Objek ini, yang dapat diperlakukan sebagai angka, adalah sangat kecil. Sebuah bilangan
dx yang kecilnya tak terhingga dapat lebih besar daripada 0, namun lebih kecil daripada bilangan apapun pada deret 1, ½, ⅓, ... dan bilangan real positif apapun. Setiap perkalian dengan kecil tak terhingga (infinitesimal) tetaplah kecil tak terhingga, dengan kata lain kecil tak terhingga tidak memenuhi
properti Archimedes. Dari sudut pandang ini, kalkulus adalah sekumpulan teknik untuk memanipulasi kecil tak terhingga.
Pada abad ke-19, konsep kecil tak terhingga ini ditinggalkan karena tidak cukup cermat, sebaliknya ia digantikan oleh konsep
limit. Limit menjelaskan nilai suatu fungsi pada nilai input tertentu dengan hasil dari nilai input terdekat. Dari sudut pandang ini, kalkulus adalah sekumpulan teknik memanipulasi limit-limit tertentu. Secara cermat, definisi limit suatu fungsi adalah:
Diberikan fungsi f(x) yang terdefinisikan pada interval di sekitar p, terkecuali mungkin pada p itu sendiri. Kita mengatakan bahwa limit f(x) ketika x mendekati p adalah L, dan menuliskan:

jika, untuk setiap bilangan ε > 0, terdapat bilangan δ > 0 yang berkoresponden dengannya sedemikian rupanya untuk setiap x:

Turunan

Artikel utama untuk bagian ini adalah:
TurunanTurunan dari suatu fungsi mewakili perubahan yang sangat kecil dari fungsi tersebut terhadap variabelnya. Proses menemukan turunan dari suatu fungsi disebut sebagai pendiferensialan ataupun diferensiasi.
Secara matematis, turunan fungsi ƒ(x) terhadap variabel x adalah ƒ′ yang nilainya pada titik x adalah:
 ,
,
dengan syarat limit tersebut eksis. Jika ƒ′ eksis pada titik x tertentu, kita katakan bahwa ƒ terdiferensialkan (memiliki turunan) pada x, dan jika ƒ′ eksis di setiap titik pada domain ƒ, kita sebut ƒ terdiferensialkan.
Apabila
z =
x +
h,
h =
x -
z, dan
h mendekati 0 jika dan hanya jika
z mendekati
x, maka definisi turunan di atas dapat pula kita tulis sebagai:

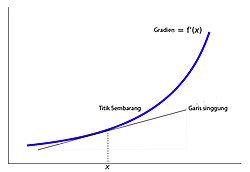
Garis singgung pada (
x,
f(
x)). Turunan
f'(
x) sebuah kurva pada sebuah titik adalah kemiringan dari garis singgung yang menyinggung kurva pada titik tersebut.
Perhatikan bahwa ekspresi

pada definisi turunan di atas merupakan gradien dari garis sekan yang melewati titik (
x,ƒ(x)) dan (
x+
h,ƒ(x)) pada kurva ƒ(x). Apabila kita mengambil limit
h mendekati 0, maka kita akan mendapatkan kemiringan dari garis singgung yang menyinggung kurva ƒ(x) pada titik x. Hal ini berarti pula garis singgung suatu kurva merupakan limit dari garis sekan, demikian pulanya turunan dari suatu fungsi ƒ(x) merupakan gradien dari fungsi tersebut.
Sebagai contoh, untuk menemukan gradien dari fungsi
f(x) = x2 pada titik (3,9):
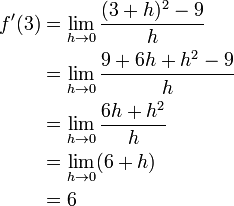
Ilmu yang mempelajari definisi, properti, dan aplikasi dari
turunan atau
kemiringan dari sebuah grafik disebut
kalkulus diferensial

Garis singgung sebagai limit dari garis sekan. Turunan dari kurva
f(
x) di suatu titik adalah kemiringan dari garis singgung yang menyinggung kurva pada titik tersebut. Kemiringan ini ditentukan dengan memakai nilai limit dari kemiringan garis sekan.
Notasi pendiferensialan
Terdapat berbagai macam notasi matematika yang dapat digunakan digunakan untuk menyatakan turunan, meliputi
notasi Leibniz, notasi Lagrange,
notasi Newton, dan notasi Euler.
Notasi Leibniz diperkenalkan oleh
Gottfried Leibniz dan merupakan salah satu notasi yang paling awal digunakan. Ia sering digunakan terutama ketika hubungan antar
y = ƒ(x) dipandang sebagai hubungan fungsional antara variabel bebas dengan variabel terikat. Turunan dari fungsi tersebut terhadap x ditulis sebagai:
 ataupun
ataupun 
Notasi Lagrange diperkenalkan oleh
Joseph Louis Lagrange dan merupakan notasi yang paling sering digunakan. Dalam notasi ini, turunan fungsi ƒ(
x) ditulis sebagai ƒ′(
x) ataupun hanya ƒ′.
Notasi Newton, juga disebut sebagai notasi titik, menempatkan titik di atas fungsi untuk menandakan turunan. Apabila
y =
ƒ(
t), maka
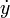
mewakili turunan
y terhadap
t. Notasi ini hampir secara eksklusif digunakan untuk melambangkan turunan terhadap waktu. Notasi ini sering terlihat dalam bidang
fisika dan bidang matematika yang berhubungan dengan fisika.
Notasi Euler menggunakan operator diferensial
D yang diterapkan pada fungsi
ƒ untuk memberikan turunan pertamanya
Df. Apabila
y =
ƒ(
x) adalah variabel terikat, maka sering kali
x dilekatkan pada
D untuk mengklarifikasikan keterbebasan variabel
x. Notasi Euler kemudian ditulis sebagai:
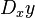 atau
atau  .
.
Notasi Euler ini sering digunakan dalam menyelesaikan
persamaan diferensial linear.
| Notasi Leibniz | Notasi Lagrange | Notasi Newton | Notasi Euler |
| Turunan ƒ(x) terhadap x | 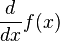 | ƒ′(x) | 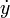
dengan y = ƒ(x) |  |







 ,
,

 pada definisi turunan di atas merupakan gradien dari garis sekan yang melewati titik (x,ƒ(x)) dan (x+h,ƒ(x)) pada kurva ƒ(x). Apabila kita mengambil limit h mendekati 0, maka kita akan mendapatkan kemiringan dari garis singgung yang menyinggung kurva ƒ(x) pada titik x. Hal ini berarti pula garis singgung suatu kurva merupakan limit dari garis sekan, demikian pulanya turunan dari suatu fungsi ƒ(x) merupakan gradien dari fungsi tersebut.
pada definisi turunan di atas merupakan gradien dari garis sekan yang melewati titik (x,ƒ(x)) dan (x+h,ƒ(x)) pada kurva ƒ(x). Apabila kita mengambil limit h mendekati 0, maka kita akan mendapatkan kemiringan dari garis singgung yang menyinggung kurva ƒ(x) pada titik x. Hal ini berarti pula garis singgung suatu kurva merupakan limit dari garis sekan, demikian pulanya turunan dari suatu fungsi ƒ(x) merupakan gradien dari fungsi tersebut.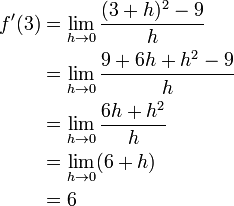

 ataupun
ataupun 
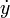 mewakili turunan y terhadap t. Notasi ini hampir secara eksklusif digunakan untuk melambangkan turunan terhadap waktu. Notasi ini sering terlihat dalam bidang
mewakili turunan y terhadap t. Notasi ini hampir secara eksklusif digunakan untuk melambangkan turunan terhadap waktu. Notasi ini sering terlihat dalam bidang 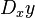 atau
atau  .
.